Les Greeks — abréviation issue des lettres grecques — sont des indicateurs qui mesurent la sensibilité des produits dérivés aux différents mouvements du marché.
Autrement dit, ils permettent d’anticiper comment la valeur d’un produit va évoluer si un paramètre précis change : le prix du sous-jacent, la volatilité ou le temps.

Ces indicateurs sont utilisés au quotidien en salle de marché pour ajuster les positions, piloter le risque et anticiper les fluctuations du marché.

Cet article propose une première approche des Greeks, avec une explication globale destinée aux lecteurs souhaitant acquérir quelques notions essentielles. Une seconde partie, plus technique et approfondie, sera publiée à la rentrée de janvier pour celles et ceux qui souhaitent aller plus loin et les maîtriser en détail.

Le Delta

Sûrement le Greek le plus connu et le plus simple à comprendre.
Le delta représente la sensibilité du prix d’une option aux mouvements de son sous-jacent.

C’est une valeur comprise entre 0 et 1 pour un call (et entre -1 et 0 pour un put), qui évolue en permanence avec le marché.

Pour faire simple :
si le delta d’un call vaut 0,5 et que le sous-jacent — par exemple une action X — augmente de 100 euros, alors la valeur du call augmentera d’environ 50 euros.

Il est important de préciser que cette relation est une approximation locale.
Le delta n’est pas fixe : il change lorsque le prix du sous-jacent évolue, ce qui signifie que cette estimation n’est valable que pour de petits mouvements du marché.

D’un point de vue plus formel, le delta est défini comme la dérivée partielle du prix de l’option par rapport au prix du sous-jacent :

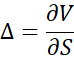
où désigne la valeur de l’option et le prix du sous-jacent.

Le Gamma

Si le delta mesure comment le prix d’une option réagit quand le sous-jacent bouge, alors le gamma mesure quelque chose d’encore plus subtil :
comment le delta lui-même change quand le sous-jacent varie.

Autrement dit, le gamma capture la “courbure” de l’option : c’est ce qui explique pourquoi, quand le marché bouge fortement, l’approximation “delta = constante” devient vite fausse.

Exemple simple : un trader est vendeur d’un call et met en place une couverture delta-neutre.
Lorsque le sous-jacent augmente, le delta de l’option progresse : il doit alors renforcer sa position sur le sous-jacent pour rester couvert.
À l’inverse, lorsque le sous-jacent baisse, le delta diminue et une partie de la couverture doit être réduite.
Plus le gamma est élevé, plus ces ajustements sont fréquents et coûteux, ce qui accroît fortement le risque opérationnel.

On comprend alors pourquoi le gamma est souvent considéré comme un risque “caché” : on peut être delta-neutre à un instant, mais ne plus l’être quelques minutes plus tard si le sous-jacent bouge.

D’un point de vue formel, le gamma est la dérivée du delta par rapport au sous-jacent, donc la dérivée seconde du prix de l’option :

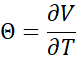
où est la valeur de l’option et  le prix du sous-jacent.

Le Theta

Le theta mesure l’impact du temps qui passe sur le prix d’une option.
Même si le marché ne bouge pas, une option perd (souvent) de la valeur à mesure qu’on se rapproche de l’échéance : c’est la time decay.

Intuition simple : une option vaut en partie parce qu’il reste du temps pour qu’un scénario favorable arrive. Plus il reste de temps, plus l’option “a une chance” de finir dans la monnaie. Quand ce temps diminue, cette chance diminue aussi.

En pratique, le theta est généralement négatif pour l’acheteur d’option (il “paie” le temps), et positif pour le vendeur (il “encaisse” le temps).

Formellement, le theta est la dérivée partielle du prix de l’option par rapport au temps :

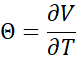
(où est la valeur de l’option et  le temps restant avant maturité ; selon les conventions, on le note parfois avec un signe négatif pour représenter la perte de valeur quotidienne).

Le Vega

Le vega mesure la sensibilité du prix d’une option à la volatilité du sous-jacent.
Plus la volatilité attendue est élevée, plus l’option a de chances de finir loin du strike (dans un sens ou dans l’autre), donc plus elle vaut cher.

Point important : le vega est généralement positif pour les calls et pour les puts.
Une hausse de volatilité augmente la valeur des options, car elle augmente l’incertitude — et l’option, c’est justement un contrat dont la valeur vient de cette incertitude.

Formellement :

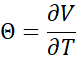
où  est la volatilité.

Le Rho

Le rho mesure la sensibilité du prix d’une option aux taux d’intérêt.
Intuitivement, les taux influencent la valeur actuelle des flux futurs : acheter plus tard à un prix fixé (strike) n’a pas la même valeur si les taux sont plus hauts ou plus bas.

En règle générale :

Pour un call, le rho est souvent positif (taux ↑ → call ↑),

Pour un put, le rho est souvent négatif (taux ↑ → put ↓).

(En pratique, le rho est souvent moins suivi que delta/vega/gamma sur les options actions “classiques”, mais il devient très important sur des maturités longues et sur les produits taux.)

Formellement :

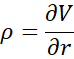
où  est le taux sans risque.